RESEARCH

Optimal design is activities on formulating the followings for a real-world design problem:

• Design variables – design factors that can be determined by the designer
• Objective function – evaluation index of the design target that should be maximized or minimized
• Constraints – conditions that the design target should satisfy

and deriving its optimal (or locally optimal) design solution by using mathematical programming, meta-heuristics, and so on.

For optimal design problems with a small number of design variables, that is, with a small degree of design freedom, it is possible to obtain the optimal solution or a quasi-optimal solution based on human intuition and experience. However, when the degree of design freedom increases, it becomes extremely difficult to obtain the optimal solution based on human intuition and experience. For example, the beginning three GIF animations show the searching process for the optimal structures of a bridge, heat radiator, and electrolyte flow channel design problems; here, structural design methodology called topology optimization is used for the solution search with hundreds of thousands of design degrees of freedom. In all cases, extremely complex optimal structures similar the morphology of living things are obtained, but it will be difficult for many people to derive these based on intuition or experience.

In today's world of global competition, design and manufacturing activities are required to be optimal, and optimal design that goes beyond the limits of human thinking can be a powerful tool. So, we will research on the followings under the key concept "optimal design".

1. Optimal design targeting integrated devices

Aiming at innovative performance improvement of integrated devices such as power semiconductor devices, optical semiconductor devices, and MEMS, we are working on research on optimal design targeting these devices.

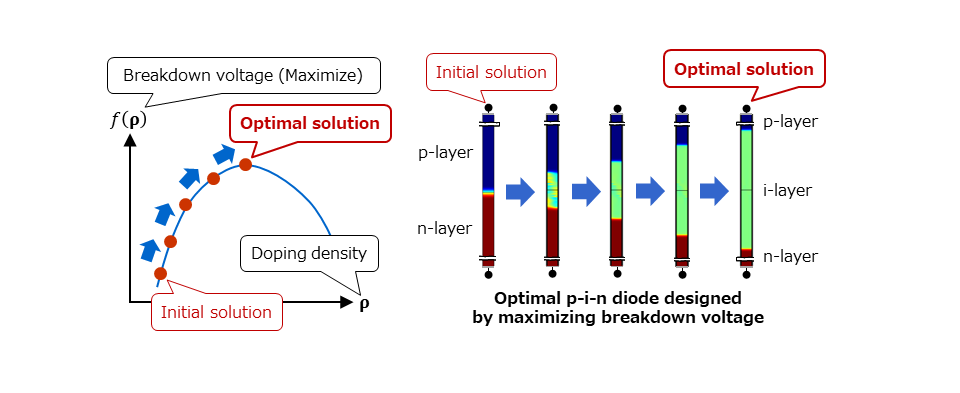
The above figure shows an example of optimal design for power semiconductor devices. In this example, doping densities in a semiconductor device are the design variables, and the breakdown voltage is maximized by topology optimization. When updating the design variables after setting a p-n diode as the initial solution, a p-i-n diode is obtained as the optimal solution. It is known that p-i-n diodes have better performance of breakdown voltage than p-n diodes, but without using such knowledge, we obtained the optimal p-i-n diode based on only mathematical procedures. This indicates the possibility of optimal design.

In this laboratory, we are working on researches to apply optimal design to design problems for more advanced and complex integrated devices.

2. Optimal design for automobiles

The electrical system of an automobile is one of typical integrated systems consisting of multiple integrated devices. In this laboratory, we regard an automobile itself, including related machine parts, as an integrated system in a broad sense, and work on researches on its optimal design for realizing innovative performance improvement.

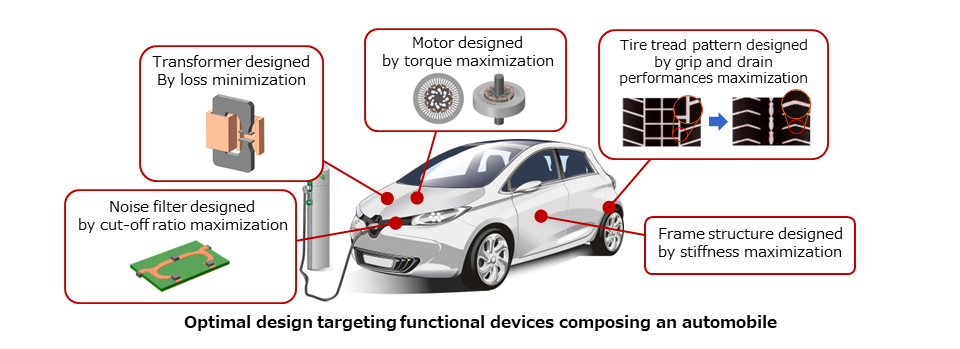
More specifically, as shown in the above figure, we work on researches on optimal design by topology optimization targeting individual functional devices that make up an automobile, and researches on optimal design at a subsystem level where these functional devices are combined.

3. Development of basic methodologies for optimal design

Research issues of optimal design are not limited to industrial applications. There are some essential and difficult problems in the academic field of optimal design. One of them is the optimal solution search for highly nonlinear optimal design problems.

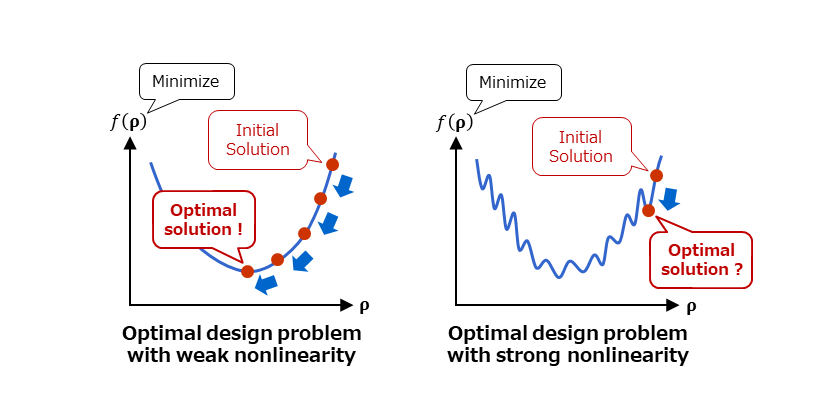
The left image shows an example of optimal design problems with weak nonlinearity, and the right image shows an example of optimal design problems with strong nonlinearity. When the nonlinearity is weak, the optimal solution search can be performed based on the sensitivity information of the objective function with respect to the design variables, but this approach does not hold for problems with strong nonlinearity. However, problems with strong nonlinearity like them just require optimal design that goes beyond the limits of human thinking.

In this laboratory, we study on researches from a view point that transcends the framework of conventional optimal design to address such essential and difficult problems; for example, we have proposed an optimal solution searching method based on deep learning that does not require sensitivity information.

4. Development of new optimal design methods inspired by living things

In the three GIF animations shown at the beginning, optimal structures similar to the morphology of living things have been obtained by the mathematical procedure. We consider that this is not a mere coincidence, but that the morphology of living things is some kind of optimal structure that has been acquired over time for adapting to the environment. Based on this hypothesis, we study on researches to elucidate the principle of morphogenesis in living things by topology optimization, and researches on new optimal design methods inspired by the mechanism of morphogenesis in living things.